PHY 115
Wave and Oscillation
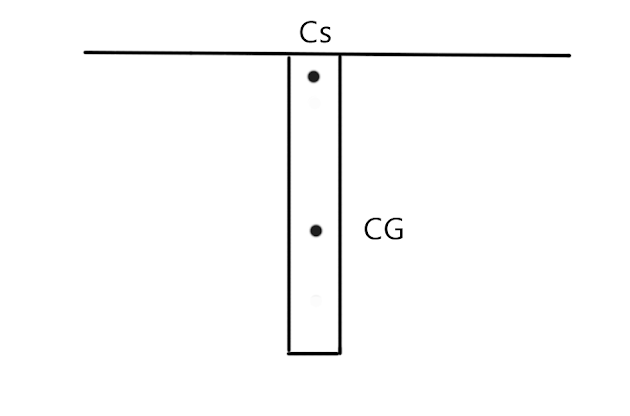
♦ Compound Pendulum: any shape rigid body...
♦ Differential Equation for Simple Harmonic Motion:
(1) Force along the string = \(Mg\cos \theta\)
(2) Force perpendiculer to the string = \(Mg\sin\theta\)
The component \(Mg\cos\theta\) balance the tension.
$$ T = Mg \cos\theta $$
The Force active on the oscillating particle is,
\begin{align*}
F = & - Mg\cos\theta \\
\textrm{when,} & \theta \rightarrow 0, ~\textrm{ the}~ \sin\theta = \theta \\
F = & - Mg\theta \tag{1}\label{eq:1}
\end{align*}
We know,
\(F = ma \tag{2}\label{eq:2}\)
The linear displacement,
\begin{align*}
y = & l\theta \\
\implies \frac{dy}{dt} = & \ \frac{d\theta}{dt} \\
\implies \frac{d^2 y}{d t^2} = & a = \ \frac{d^2 \theta}{d t^2} \tag{3}\label{eq:3}
\end{align*}
Comparing equation (1) and (2),
$$ F = Ml \frac{d^2 \theta}{d t^2} $$
Now using equation (1)
\begin{align*}
& Ml \frac{d^2 \theta}{d t^2} = - Mg\theta \\
\implies & \frac{d^2 \theta}{d t ^2} + \frac{g}{l}\theta = 0
\end{align*}
comparing with differential equation of SHM,
\begin{align*}
& \omega^2 = \frac{g}{l} \\
\implies & \left(\frac{2\pi}{T } \right)^2 = \frac{g}{l} \\
\implies & t = 2 \pi \sqrt{\frac{l}{g}}
\end{align*}
HW: Find out T for compound pendulum.




Post a Comment